マルチバースとよく似た概念「多世界解釈」
本連載ではこれまで、宇宙全体を研究の対象とする「宇宙論」の分野における「宇宙は無数に存在する」というマルチバースの仮説について紹介してきた。一方、宇宙論とは対照的に、ミクロな世界を扱う「量子力学」の分野でも、実は「世界は無数に存在する」という一見よく似た考え方が登場する。「多世界解釈」と呼ばれるものだ。
マルチバース宇宙論と量子力学の多世界解釈はこれまで全く別々のものだと考えられてきたが、近年、両者を結びつける新しい考え方が注目を集めている。今回は、多世界解釈とはどういうものなのか、そしてマルチバース宇宙論とどのようにつながっているのかについて紹介しよう。
量子力学誕生前の物理学者たちの世界観「未来は決まっている」
量子力学とは、ミクロな世界の電子や原子、光などの性質を解き明かすために、1900年ごろに産声を上げた理論である。量子力学は現代物理学の土台となっている理論であり、現代の様々なテクノロジーの基礎にもなっている。例えば、半導体の仕組みは量子力学に基づいて考える必要があり、スマホやパソコンなどのIT機器は量子力学が産んだとも言える。
量子力学は当時、非常に革命的な理論であり、その誕生によって物理学者たちの世界観は大きく変わることになった。量子力学は、それまで物理学者たちに支持されていた「決定論的な世界観」を覆したのだ。
決定論的な世界観とは、簡単に言うと、「未来は決まっている」という考え方のことである。この考え方は、主に「ニュートン力学」を土台にしている。ニュートン力学とは、アイザック・ニュートン（1642～1727）が確立した物理学の理論で、物体が力を受けてどのように運動するかを説明する理論である。中学校や高校で習う力学は、ニュートン力学だ。
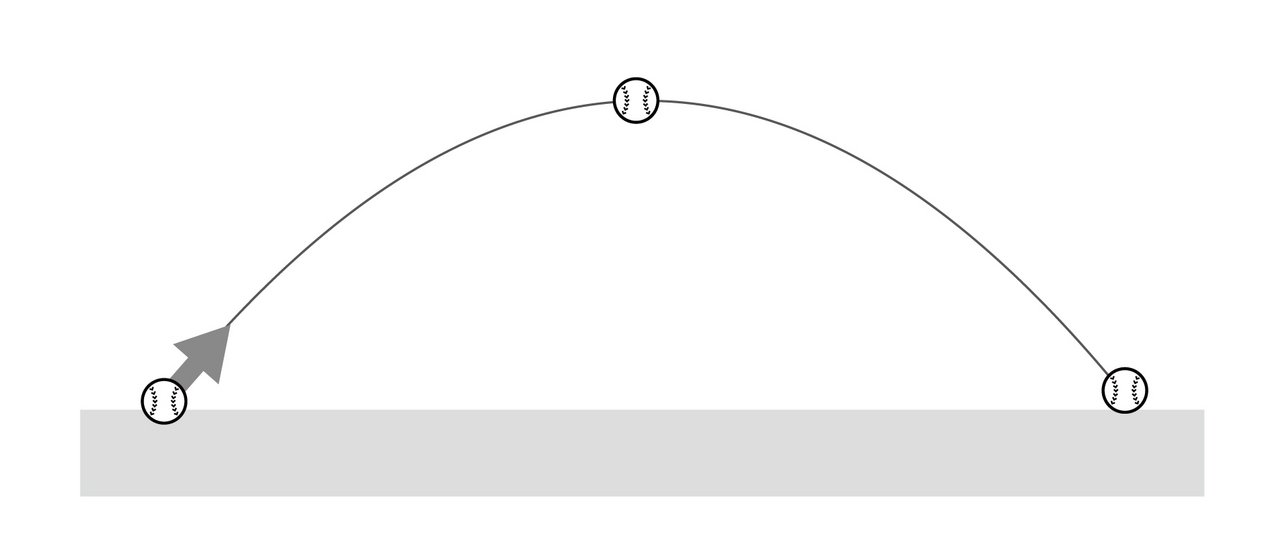
例えば、ボールの遠投を考えてみよう。空気の影響が無視できる場合、最初にボールを投げるときの角度、そして速さ（初速）を決めると、ボールがどのような軌跡を描いて飛んでいき、何メートル先の地面に落下するかが正確に予測できる（図1）。つまり、ボールを投げた時点で、ボールの未来は既に決まっている、ということになる。
実際のボールは、空気抵抗や風などの影響を受けるので、ボールの運動を正確に予測することはそれほど簡単ではないが、そのときの空気の状態を正確に知ることができれば、原理的にはボールの運動は正確に予測できるはずだ。
ボールだけではない。例えば、サイコロを振ってどの目が出るかも、原理的には予測できるはずである。サイコロの出る目は「確率的」で、予測はできないと普通は考えるが、それはサイコロの状態を正確に知ることが極めて困難だからだ。しかし、サイコロを投げる角度や速さ、回転のかけ方、サイコロとテーブルの間の反発係数（衝突前後で速さがどう変化するかを表す値）、そのときの空気の状態などが正確に分かれば、原理的には、サイコロがどう運動するかはニュートン力学に基づいて正確に予測できるはずなのだ。
ニュートンよりも少し後の時代の物理学者、ピエール=シモン・ラプラス（1749～1827）は、以上のような考え方をもとにして、「ある瞬間において、宇宙のあらゆる物体の状態（位置や速度など）が分かれば、未来を完全に予測できる」と主張した。ある瞬間における、あらゆる物体の状態を知っている仮想的な存在は、「ラプラスの悪魔」と呼ばれる。ラプラスの悪魔にとってみれば、未来は決まっていることになる。
現在の物体の状態が正確に分かれば、ニュートン力学を使って過去の状態を知ることもできる。例えば、先ほどのボールの遠投の場合、ボールが地面に落下する直前の運動状態を正確に知ることができれば、ボールがどのような軌跡を描いて飛んできたかを時間を遡って知ることもできるのだ。つまり、ラプラスの悪魔にとってみれば、宇宙の歴史は完全なる一本道だということになる。
以上が、量子力学誕生前の物理学者たちの決定論的な世界観である。
ミクロな粒子は観測するまで位置が決まっていない
この決定論的な世界観を覆したのが量子力学だ。量子力学によると、ミクロな世界は確率に支配されており、未来を正確に予測することは不可能だとされる。これはどういうことだろうか？
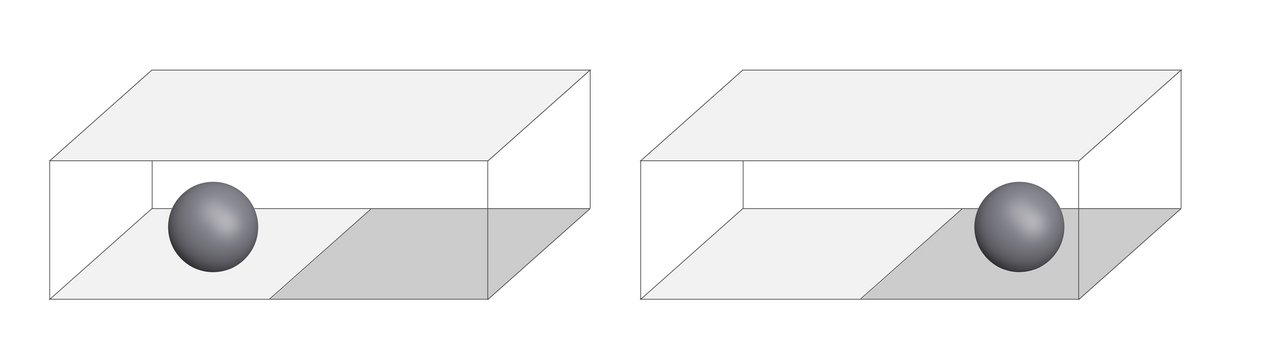
箱に入ったボールを考えよう（図2）。ボールが箱の中の左半分、または右半分のどちらにあるかは、箱を開けてみないと分からないとする。
これが普通のボール、つまり日常生活で見るようなマクロなサイズのボールであれば、箱を開けたときに左にボールがあれば、それは箱を開ける前から左にあったということになる。
しかしミクロな物体、例えば、電子で同じような実験を行った場合、量子力学では、箱を開けるまで電子が左右のどちらにいるかは決まっていないと考える。量子力学で予測できるのは、「左で発見される確率は30％、右で発見される確率は70％」といったように発見確率だけだ。箱を開ける前は、電子が左にいる状態と右にいる状態の「重ね合わせ状態」になっていると考える。そして箱を開けて電子の位置を「観測」した瞬間、電子の位置が確定し、電子は左か右のどちらかに姿を現すことになる。このとき電子がどちらに姿を現すかは偶然によって支配されている。
量子力学について初めて聞いた人からすれば、以上の議論は極めておかしなものに聞こえるだろう。「箱を開ける前も、電子は左右のどちらかにいたはずだ。それを人間側が知らないだけだ」。そう考えるのが普通だ。しかし量子力学によると、この電子について知り得るすべての情報を得たとしても、観測前には電子の位置は決まっておらず、観測によって初めて位置が決まるのである。
観測によって初めて決まるというのは、電子の位置だけの話ではなく、運動量（質量×速度）やスピン（自転の勢いに相当する物理量）など、電子が取り得るさまざまな状態についても同様である。
これは単なる哲学的な議論ではない。物理学、つまり科学の話である。「電子の位置などの状態は観測前には決まっておらず、観測によって初めて決まる」ということは、数々の実験で検証され、正しいことが確かめられているのだ。
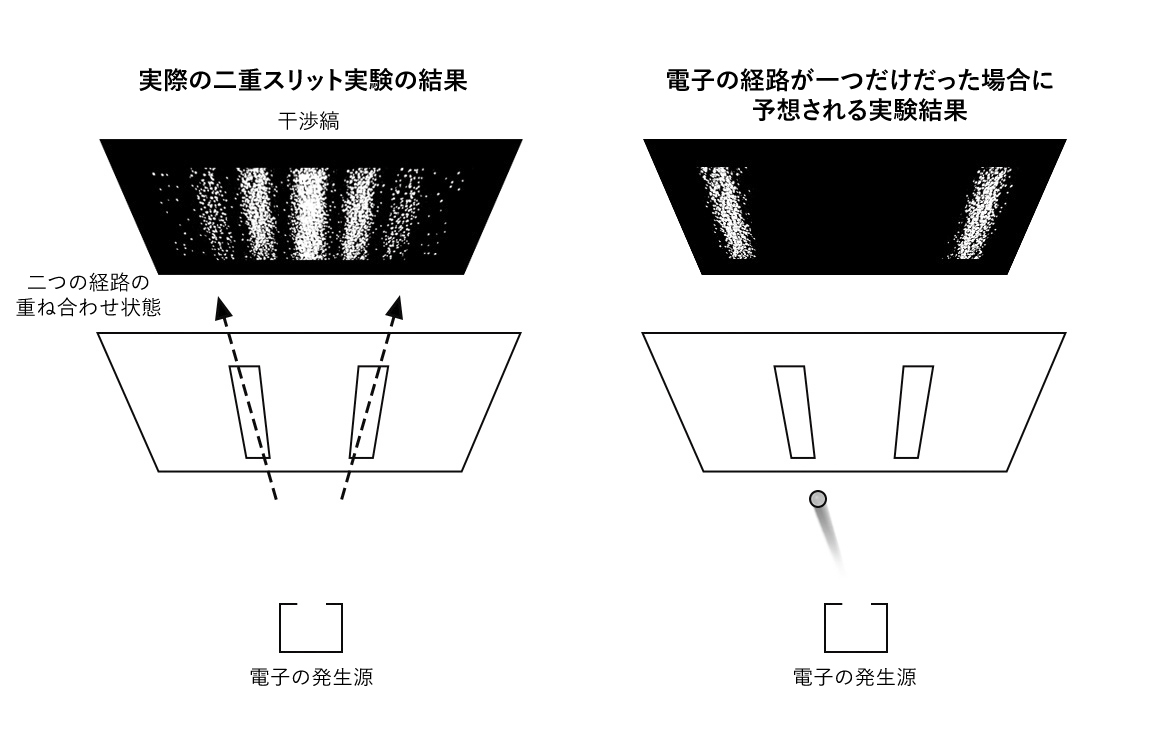
例えば、「二重スリット実験」と呼ばれる実験では、一つの電子が経路Aを通った状態と、経路Bを通った状態が互いに影響を及ぼしあうことが実験によって確かめられている（図3）。二重スリット実験では、電子がどちらか一方の経路しか通っていないと考えると、実験結果をうまく説明できないのだ(1)。
観測される電子は、1回の電子の発射につき一つだけであるにもかかわらず、観測されていない間は、電子はあたかも分身の術を使ったかのように複数の状態（位置や経路など）を取ることができ、その分身どうしは互いに影響を及ぼしあうことができるのだ。分身どうしの影響の及ぼしあいは「干渉」と呼ばれる。
観測によって起きる「状態の収縮」とは？
以上をまとめると、観測前の電子は複数の状態を同時に取っており（重ね合わせ状態になっており）、観測することによって一つの状態に確定する。そしてどの状態が観測されるかはランダムであり、確率によってしか予測できない――ということになる。このような量子力学の解釈は「コペンハーゲン解釈」と呼ばれる。このような解釈の指導的な立場にあったニールス・ボーア（1885～1962）が、デンマークのコペンハーゲンにいたことに由来している。
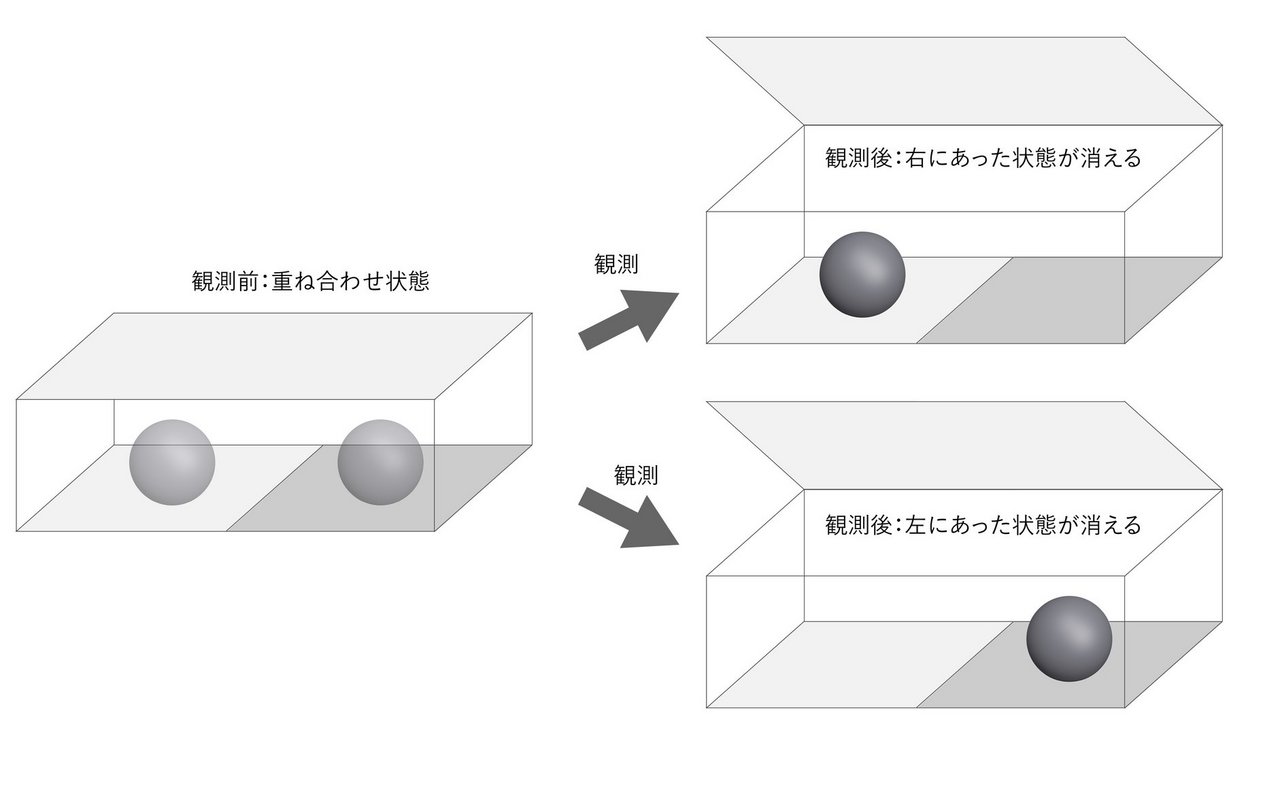
コペンハーゲン解釈では、例えば、箱の中の電子が左側で観測されたとすると、観測前にあった「電子が右側にあった状態」は消え去ったと考える（図4）。このように、もともとあった複数の状態が観測によって一つの状態に決まることは「状態の収縮」と呼ばれる。
コペンハーゲン解釈は当時、物理学者たちの間で大論争を巻き起こした。特に有名なのは、アルベルト・アインシュタイン（1879～1955）からの反発だ。アインシュタインは量子力学の構築にも多大なる貢献をした人物だが、そのアインシュタインがコペンハーゲン解釈を痛烈に批判したのである。アインシュタインは「神はサイコロを振らない」という有名な言葉を残している。サイコロは確率を象徴したものであり、アインシュタインは「自然界は確率に支配されている」と考える量子力学の解釈に、最後まで納得しなかったのである。
量子力学によると、電子などのミクロな粒子は「シュレーディンガー方程式」というものに従って運動する。シュレーディンガー方程式を数学的に解くことによって、例えば、電子の状態がどのように時間的に変化していくかを予測することができるのだ。
しかし観測によって起きる状態の収縮は、シュレーディンガー方程式から導くことはできない。つまりコペンハーゲン解釈は、シュレーディンガー方程式に加えて、「観測によって状態の収縮が起きる」という仮定を組み込んで、ミクロな粒子の振る舞いを説明する解釈だということになる。
ところで観測とは、どの時点のことを言うのだろうか？ 箱の中の電子の場合、光を当てたときだろうか？ それとも電子に当たって跳ね返った光が検出器と相互作用したときだろうか？ それとも検出器が電子の位置の測定結果を表示してそれを観測者が認識したときだろうか？ このことについては明確な答えは出ていない。ただし、私たちが日常生活で目にするマクロな物体は重ね合わせ状態にはなっていないように見えるので、電子がマクロな物体に影響を及ぼしたどこかの時点で、状態の収縮が起きるのだろうと考えられている。
なお、コペンハーゲン解釈は現代においても、量子力学の標準的な解釈だとされている。ただし、物理学者自身がどの解釈を支持しているかを明確にするケースは（特に日本では）そう多くはないので、昔ながらのコペンハーゲン解釈を支持している物理学者がどれくらいいるかはよく分からない(2)。
可能性の数だけパラレルワールドが実在している？
一方、「状態の収縮」は余計な仮定であり、量子力学はシュレーディンガー方程式だけに基づいて考えるべきだとする、新たな解釈を提唱する物理学者が現れた。1957年にその革命的な論文を発表したのは、アメリカ、プリンストン大学の大学院生だったヒュー・エヴェレット3世（1930～1982）である。エヴェレットの解釈は後にブライス・ドウィット（1923～2004）らによってさらに磨き上げられ、今日では「多世界解釈」と呼ばれている。
コペンハーゲン解釈は、量子力学が適用される電子などのミクロな存在と、観測装置や観測者などのマクロな存在を明確に分ける考え方だとも言える。重ね合わせ状態にあったミクロな物体は、マクロな物体との接触によって状態の収縮が起きる、と考えるからだ。
一方で多世界解釈では、ミクロとマクロの区別は考えない。マクロな物体も電子や原子などのミクロな粒子が集まってできているのだから、量子力学の対象とみなすべきだと考えるのだ。そして電子のようなミクロな粒子と、観測装置や観測者を含めた世界全体をセットで考える。また、多世界解釈では、状態の収縮を考えないので、上述の箱の中の電子の例で言えば、観測後も、「電子が左側で発見された状態」と「電子が右側で発見された状態」が消えずに残ると考える。
しかし観測者は、電子を左側に発見するか、右側に発見するかのどちらかである。そこで、多世界解釈では、世界が「電子が左側で発見された世界」と「電子が右側で発見された世界」に枝分かれすると考える。「電子が左側で発見された世界」では、検出器のディスプレイは電子が左側にあったことを示し、観測者は電子が左側にあったと認識する。「電子が右側で発見された世界」では、検出器のディスプレイは電子が右側にあったことを示し、観測者は電子が右側にあったと認識する。多世界解釈では、このような二つの世界がともに「実在する」と考えるのだ。
そしてこれら二つの世界は、共存しつづける。二つの世界はそれぞれ独自に歴史を紡いでいくことになるわけだ。
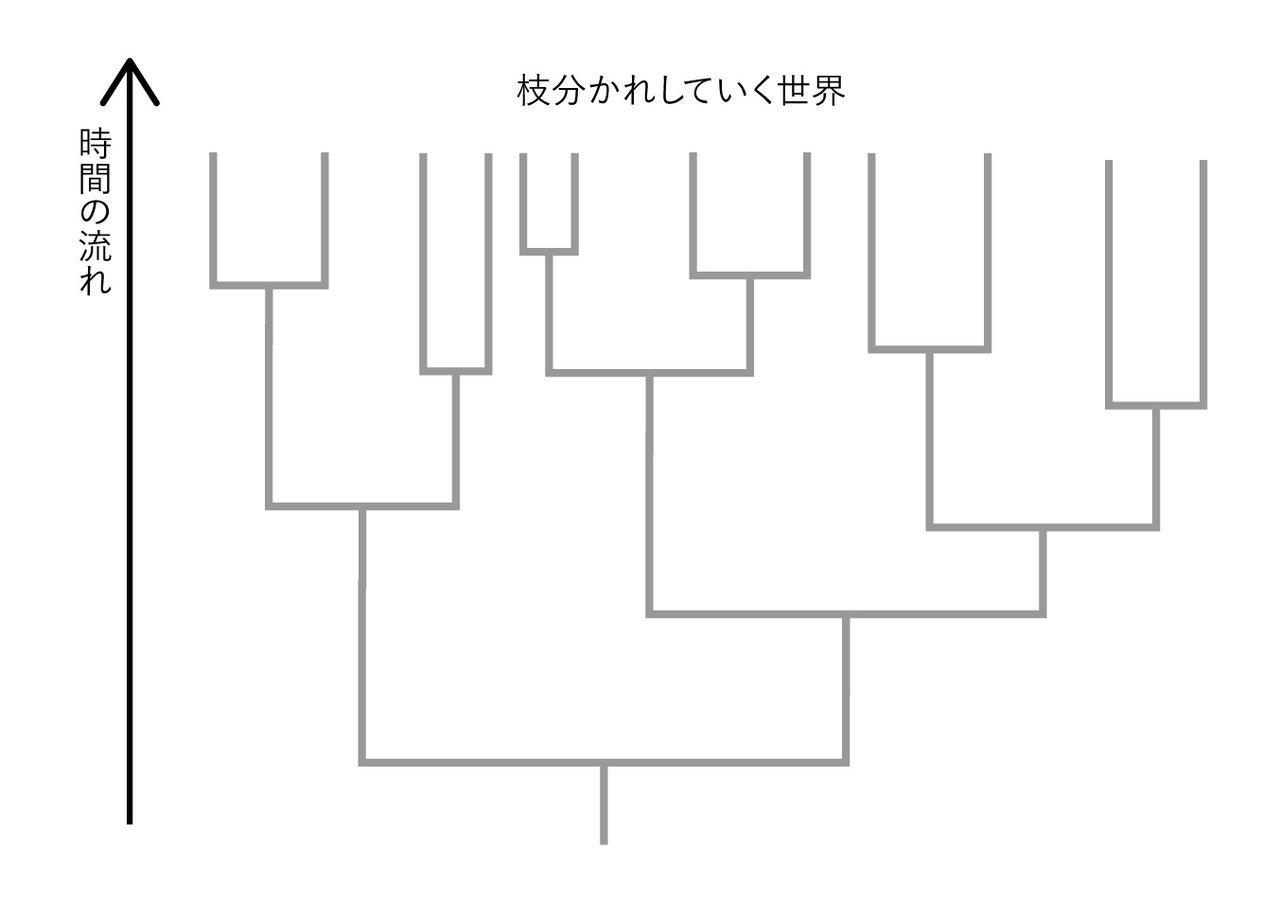
多世界解釈によると、このようにして世界は次々と枝分かれしていくことになる。多世界解釈はこういった並行世界、いわゆるパラレルワールドの存在を認める解釈なのである。
SF作品では、複数のパラレルワールドを登場人物が行き来するシーンが描かれることもあるが、残念ながら量子力学の多世界解釈に基づいたパラレルワールドではそのようなことはできない。マクロなレベルで違いが生じて枝分かれした後のパラレルワールドどうしは、事実上、断絶するのだ。枝分かれした世界どうしが互いに影響を及ぼしあう確率（干渉を起こす確率）は、ほぼゼロになるのである。
多世界解釈によると、ありえた可能性の数だけ並行世界が存在することになる。あなたとは少し違う人生を歩んでいるあなたもそこにいるかもしれない。ただし、世界が枝分かれするには、その前に量子力学的な重ね合わせ状態が実現している必要がある。私たちの人生にどれだけ量子力学的効果が関わっているのかはよく分かっていないので、実際にどのような並行世界が存在しているのかは明らかではない(3)。
ちなみに、2020年にノーベル物理学賞を受賞した、著名な数学者であり物理学者でもあるロジャー・ペンローズは、私たちの脳の情報処理には量子力学的な効果が関わっているとする「量子脳理論」を提唱している。もしこの考え方が正しいのなら、私たちが何かの判断を行うたびに世界が枝分かれしているのかもしれない。ただし、ペンローズの理論はあくまで仮説の一つであり、広く支持されているとは言えないようだ。
ところで先ほど「決定論的な世界観を覆したのが量子力学だ」と述べたが、実は多世界解釈は広い意味での決定論的な世界観を維持する考え方だと言える。枝分かれする無数の世界を含めた全体で見れば、未来はシュレーディンガー方程式によって決まっていると言えるからだ（図6）。ただし、個々の世界の観測者からすれば、未来が予測不能であること（自分がどの枝の世界に行くか予測不能であること）には変わりはない。
多世界解釈の最初の論文は、大学院生による博士論文だった
エヴェレットが多世界解釈についての論文を書いたとき、彼はまだ大学院生だった。多世界解釈について世界で初めて書かれた論文は、エヴェレットが博士号をもらうために書いた論文だったのだ。
エヴェレットの指導教官は、ブラックホールという言葉を世に広めたことでも知られる著名な物理学者ジョン・ホイーラー（1911～2008）だった。エヴェレットの論文はあまりに革新的な内容だったため、ホイーラーとの長く激しい議論を通して、元の4分の1ほどの長さにまで削られ、最終的に博士論文として提出されたものは多世界解釈につながる重要なエッセンスが取り除かれたものになってしまった。そのため、エヴェレットはその論文の内容に満足していなかったとされる。
短くなった博士論文は、同じ1957年、Reviews of Modern Physics誌に掲載されたが、大きな注目を集めることはなかった。失望したエヴェレットは物理学の研究の道には進まず、軍事研究の道へと進むことになる。
その後、1973年にドウィットらが『The Many-Worlds Interpretation of Quantum Mechanics（量子力学の多世界解釈）』という本を出版し、その中で、短くされる前のエヴェレットの論文を掲載した。こうしてようやく多世界解釈は広く世に知られるようになっていく。
多世界解釈は「観測によって状態の収縮が起きる」という仮定を必要としない
物理学者に限らず、科学者たちが何らかの理論を構築していくなかで、大きな指針とする考え方の一つに「オッカムのかみそり」というものがある。「ある現象の仕組みを説明するために仮定が少ない理論ほど優れている」という考え方だ。これは14世紀に活躍したイギリスの哲学者オッカム（オッカムのウィリアム）の考え方に由来し、「思考節約の原理」などとも呼ばれる。
たとえば、「初詣で宝くじが当たるように祈ったら、宝くじで100万円が当たった」と誰かが述べたとしよう。この場合、オッカムのかみそりの考え方では、祈ろうが祈るまいが宝くじが当たる可能性はもともとあったので、「初詣で宝くじが当たるように祈ったら」という文言は余計であり、バッサリと切り落とすべきだということになる。
さて、量子力学のコペンハーゲン解釈は、シュレーディンガー方程式に加えて、状態の収縮という仮定を必要とする解釈だ。一方で多世界解釈は状態の収縮を考えない。つまり多世界解釈の支持者からすれば、この解釈は仮定が少なく、オッカムのかみそりの考え方に従えば、コペンハーゲン解釈より優れた解釈である、ということになる。
しかし、多世界解釈を支持しない物理学者たちからすれば、状態の収縮という仮定を一つ減らせたとしても、無数の並行世界の存在を認めるということには大きな抵抗があるようだ。
量子コンピューターは並行世界を利用して超高速計算を実現?
多世界解釈は、本連載の第3回で紹介したような宇宙の誕生の研究と相性がいい。ミクロなサイズの宇宙が「無」から誕生するといったことを理論的に研究する場合、量子力学の効果を考える必要があるが、宇宙の外に観測者はいないので、コペンハーゲン解釈では考えにくい。
一方で、多世界解釈では観測者が必要ないので、宇宙の始まりを量子力学にもとづいて考えやすいのだ。実際1980年代には、「『無』からの宇宙創成論」などの宇宙誕生についての研究が活発になり、多世界解釈も脚光を浴びるようになった。
また、1985年に「量子コンピューター」の基礎となる理論を打ち立てたことで知られるデイヴィッド・ドイッチュも多世界解釈の支持者として知られている。ドイッチュは多世界解釈にもとづいて量子コンピューターの原理を考案したそうだ。
量子コンピューターとは、重ね合わせ状態などの量子力学的な効果を利用することで、問題によっては従来のコンピューターを圧倒的に上回る速さで計算できる未来のコンピューターである。ドイッチュ流に言えば、「量子コンピューターは、並行世界で分担して計算を行うことで超高速計算を実現している」ということになる。量子コンピューターなどの量子情報技術の研究は近年活発化しており、その流れで多世界解釈の支持者が増えているとも言われている。
ただし、量子コンピューターの原理はコペンハーゲン解釈などの他の解釈で考えることもできるので、量子コンピューターが実用化されたとしても、多世界解釈が証明されたことにはならない。
「別の泡宇宙」は確率空間の中に存在する?
さて、本連載で取り上げてきた永久インフレーションにもとづいたマルチバース宇宙論に登場する「別の泡宇宙」は、空間的には私たちが住む泡宇宙とつながっていた。つまり「遠い世界」の話だった。
一方で多世界解釈に登場する「別の世界」は、まさに私たちの目の前の話、つまりココの話だ。別の世界は目の前にあるはずなのに見えないし、触れもしない。私たちの住む世界とは事実上、関わり合いをもたなくなってしまっているのである。
以上のことから分かるように、量子力学の多世界解釈と、永久インフレーションに基づいたマルチバースは本来、別の話だ。
しかし本連載の監修者である野村泰紀に加え、レオナルド・サスキンドやラファエル・ブッソは、2011年ごろ、それぞれ独立に多世界解釈とマルチバースがある意味で同じものである可能性を理論的に示している。これはいったいどういう意味なのだろうか？
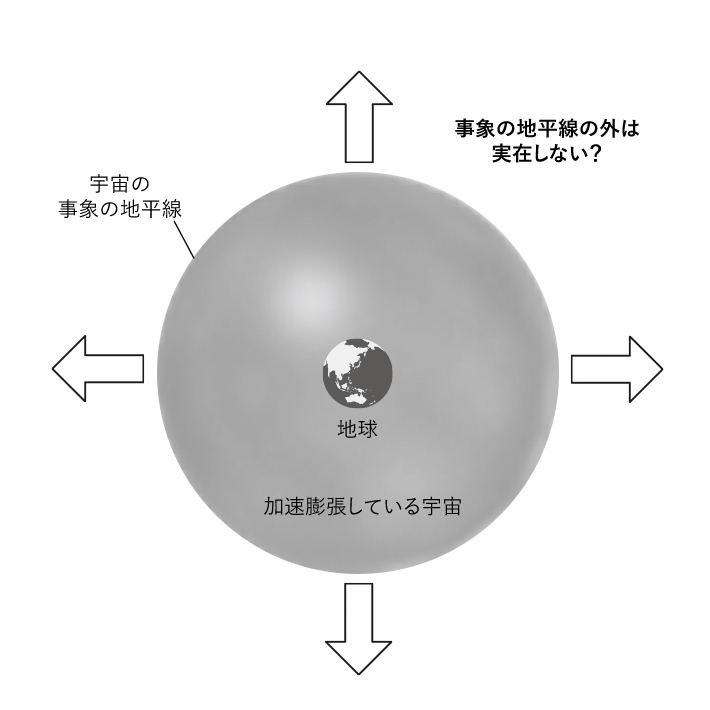
連載の第7回で紹介したように、私たちの宇宙の膨張は加速している。地球からある距離より遠い場所は、地球から見て光速を上回る速度で遠ざかっているが、加速膨張している宇宙ではそういった場所から放たれた光は未来永劫、地球には届かないことになる（図7）。このような境界面は、宇宙における「事象の地平面（event horizon）」と呼ばれている(4)。
光速は宇宙の最高速度なので、事象の地平面より外からは、どんな影響も未来永劫、地球には及ばないことになる。野村によると、地球にいる観測者にとって、事象の地平面より外側は単に「我々と無関係」というだけではなく、「存在しない」ことになる。逆に「存在しない」と考えないと、マルチバースで起きる現象の確率の計算が破綻してしまうのだという。
永久インフレーションを起こしているマルチバースでは、インフレーションが終わらないため、無限の時空が生成される。無限の時空の中では、どんなに起きる確率が低い現象でも無限回起きる。ある事象Aが起きる確率は、「事象Aが起きる回数÷全体の回数」で計算されるが、無限の大きさをもつマルチバースでは、この分母も分子も無限大になってしまい、計算不能になってしまうのだ(5)。
しかし、この考え方が正しければ、本連載でこれまでに紹介してきたマルチバース、すなわち無数の宇宙が存在しないことになってしまう。無数の宇宙が存在しないと、連載の第6回と第7回で紹介した「物理定数の微調整問題」も解決できなくなる。
ここで登場するのが量子力学の多世界解釈だ。野村によると、無数の宇宙は私たちが住む泡宇宙と“地続き”に存在しているのではなく、多世界解釈にもとづいた「確率空間」の中に存在していると考えることができるのだという。
前回紹介したように、泡宇宙は親宇宙から、「トンネル効果」という量子力学的な現象によって誕生する。つまり、泡宇宙の誕生は量子力学的な現象であって、多世界解釈によると、その際には世界の枝分かれが起きることになる。「親宇宙の中に泡宇宙Aが誕生した世界」と「泡宇宙Aが誕生しないままの世界」が枝分かれするのである。
従来のマルチバース宇宙論によると、親宇宙の中のあちこちにトンネル効果によって無数の泡宇宙が誕生する（図8）。一方、多世界解釈に基づいたマルチバース宇宙論（量子マルチバース宇宙論）では、様々な時間、様々な場所で泡宇宙が誕生したそれぞれの世界が「確率空間」の中で共存していると考える。量子マルチバース宇宙論の視点では、図8のような従来のマルチバースの描像は、確率空間に存在する無数の世界をつぎはぎして人為的に作られたものだということになる。
従来のマルチバースの描像が正しいのか、それとも量子マルチバースの描像が正しいのか、はたまたマルチバースは物理定数の微調整問題などを解決するために物理学者たちが考え出した幻想なのか……。その答えはまだ得られていない。
さて、次回からは、マルチバース宇宙論の土台となっているインフレーション理論や超ひも理論の検証可能性について考えていこう。果たしてこれらの理論は、近い将来に天文観測や実験によって実証することはできるのだろうか。
第9回の要点
- ミクロな世界の物理学である量子力学には、さまざまな解釈がある。
- 量子力学の解釈の一つ「多世界解釈」によると、世界は時々刻々と枝分かれしており、可能性の数だけ、無数の並行世界が存在していることになる。
- 多世界解釈に基づいた量子マルチバース宇宙論によると、無数の宇宙は私たちの世界と地続きではなく、「確率空間」の中に存在している。
注
- もう少し詳しく説明すると、電子は観測前（スクリーンに到達する前）は波として振る舞う。左のスリットを通った電子の波と、右のスリットを通った電子の波が重なり合い（干渉し合い）、強め合ったり弱め合ったりすることで干渉縞が生じる。
- 近年は、コペンハーゲン解釈に「ベイズ確率（ベイズ統計）」という数学の考え方を取り入れた「量子ベイズ主義（QBism）」も注目を集めている。この解釈では、量子力学に登場する確率を「観測者の主観的な信じる度合い」だと考える。
- 量子力学的な重ね合わせ状態を利用して乱数を発生させる「量子乱数発生器」という装置があるが、これを使えば、異なる人生を歩む複数のあなたを作り出すことができる（多世界解釈が正しければ、だが）。事前にどんな値が出たら、どう行動するかを決めておき、その後、量子乱数発生器に乱数を生成させる。多世界解釈によると、乱数の生成に伴って世界が枝分かれするので、それぞれの世界で異なる行動をするあなたが生じることになる。
- ブラックホールの表面も「事象の地平面」と呼ばれる。ブラックホールの場合も、事象の地平面より内側から放たれた光は未来永劫、事象の地平面より外に出ていくことはできない。これは強い重力によって、光がブラックホールの中心に向かって引っ張られていくためだ。
- 例えば、確率の計算における分母と分子が比例関係にあった場合、そこから極限を考えることができたら、有限の確率を得ることができる（lim［x→∞］ x/ax=1/a）。しかし無限の時空を生成するマルチバースでは、そのような計算がうまくできないことが知られている。