宇宙は有限？ 無限？

前回の「宇宙はどのくらい広いのか」では、宇宙の大きさは有限である可能性も、無限である可能性もあり、どちらであるかは結論が出ていない、という話をした。今回は有限の宇宙と、無限の宇宙がそれぞれどのようなものなのかを深掘りしていこう。まずは「有限の宇宙」についてだ。

よく誤解されがちなのだが、宇宙が有限であったとしても、必ずしも宇宙空間に果て⁽¹⁾があることにはならない。宇宙空間に果てがなくても、宇宙が有限になることがあるのだ。この辺りは非常に重要なので、ゆっくりと説明していこう。

「宇宙空間に果てがないんだったら、宇宙は無限のはずだ」と思うかもしれない。だが、実はそうではない。こういった問題を考える上で、言葉の定義は非常に重要なので、まずは本記事での「有限の宇宙」、「無限の宇宙」の意味を明確にしておこう。

空間がある場所で突然途切れているような「果てのある有限の宇宙」は、ありえないとは言えないが、かなり特殊なものなので⁽²⁾、本連載では扱わない。本連載でいう有限の宇宙とは、「体積が有限で、果てがない空間」のことを指すことにしよう。「体積が有限で、果てがない空間」そのものはなかなか想像しにくいので、1つ次元を減らして、「有限の2次元の宇宙」を考えてみよう。つまり、「面積が有限で、果てがない面」である。このような面は無数に考えられるが、最も単純なのは地球の表面のような「球面」である。

球面の面積は、当然ながら有限だ。しかし球面の上をどこまで進んでいっても、何かにぶつかることはないし、面が突然途切れていることもないので、「果てがない」といえる。つまり、曲がって閉じている面であれば、「面積が有限で、果てがない面」になるわけだ。

ここから類推すると、「体積が有限で、果てがない空間（＝有限の宇宙）」とは、曲がって閉じている空間ということになりそうだ。では、「曲がった空間」とは何なのだろうか。そんなものがありうるのだろうか。

結論から先に言うと、アルベルト・アインシュタイン（1879～1955）が1915年ごろに確立した「一般相対性理論」という物理学の理論によって、「空間は曲がりうる」ということが分かっている。しかも、空間が曲がることは、理論上だけの話ではなく、実際に天文観測などによって実証されているのだ。

では、どうすれば、空間が曲がっていることを確かめることができるだろうか？　空間の曲がりを検証するために使われるのは「光」である。光は本来、まっすぐ進む性質があるため、もし真空の宇宙空間で光が曲がって進んだとしたら、それは空間自体が曲がっていることになるのだ。

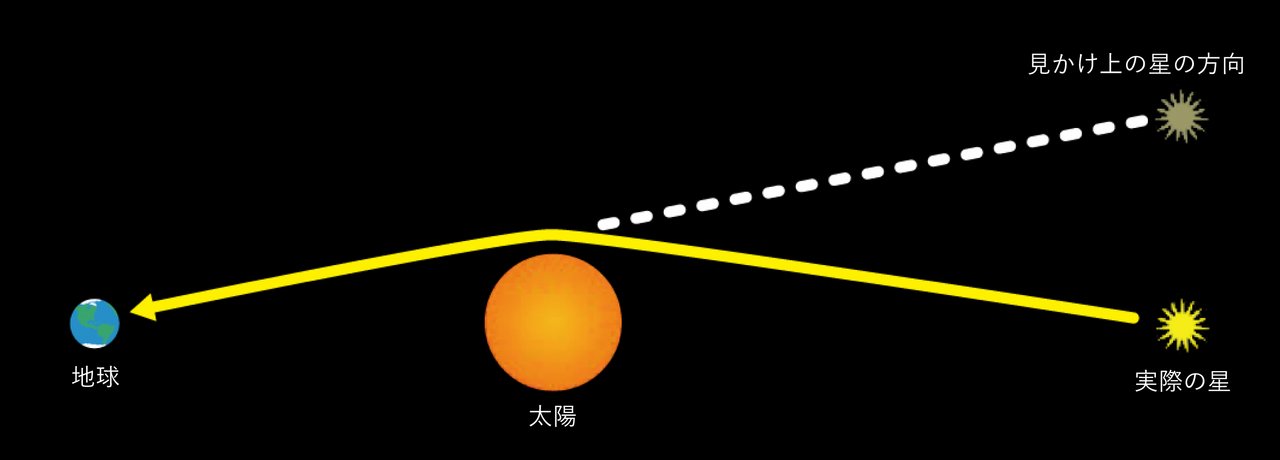
一般相対性理論によれば、質量⁽³⁾をもった物体の近くでは空間が曲がる。そして、物体の質量や密度が大きいほど、空間の曲がり方は大きくなる。例えば、太陽の近くでは、空間が曲がっていることが実際に確かめられている。太陽の後ろの方向にある遠い星からやってきた光が、太陽の近くで曲げられて地球に届くことが、イギリスの天文学者・物理学者アーサー・エディントン（1882～1944）によって1919年に確認されているのだ（図1）。光が曲げられた結果、星の見かけの位置がわずかにずれたのである（ずれは角度にして1.75秒角。1秒角は1度の3600分の1）。なお、通常、太陽の近くの星は、太陽の明るさにかき消されて見えないが、この観測は月が太陽を隠す皆既日食のときに行われた。

このような現象は「重力レンズ効果」と呼ばれている。空間のゆがみがレンズのように振る舞うわけだ。特にこのようにリング状に見える像は「アインシュタイン・リング」と呼ばれている。宇宙では、重力レンズ効果は特に珍しい現象ではなく、似たようなゆがんだ銀河の像はたくさん見つかっている。

「空間が曲がる」なんてことは、私たちの常識的な感覚からすると、にわかには信じがたい話だ。しかし「空間が曲がる」ということは、多数の天文観測によって既に実証されており、現代科学では、疑いようのない事実だとみなされている。常識的な感覚にしばられていては、自然界の真理に近づくことはできないのだ。

さて、もう一度、地球の表面のような球面を考えてみよう。球面となっている地面に沿ってまっすぐに進みつづけると、最終的には地球をぐるっと1周して元の場所に戻ってくるはずだ。ここで注意したいのが、球面上の「まっすぐ（直線）」とはどういう意味か、である。球面上の直線は3次元空間から見ると曲がっているので、改めて球面上での直線の定義を考えなくてはならない。

答えを先に言ってしまうと、球面上の「まっすぐ」とは、「球面に沿って2点間を結んだ最短ルート」という意味である。例えば、2点間にゴムをピンと張ると、ゴムは球面上の最短ルートを描く。つまり、球面上の直線になるわけだ。

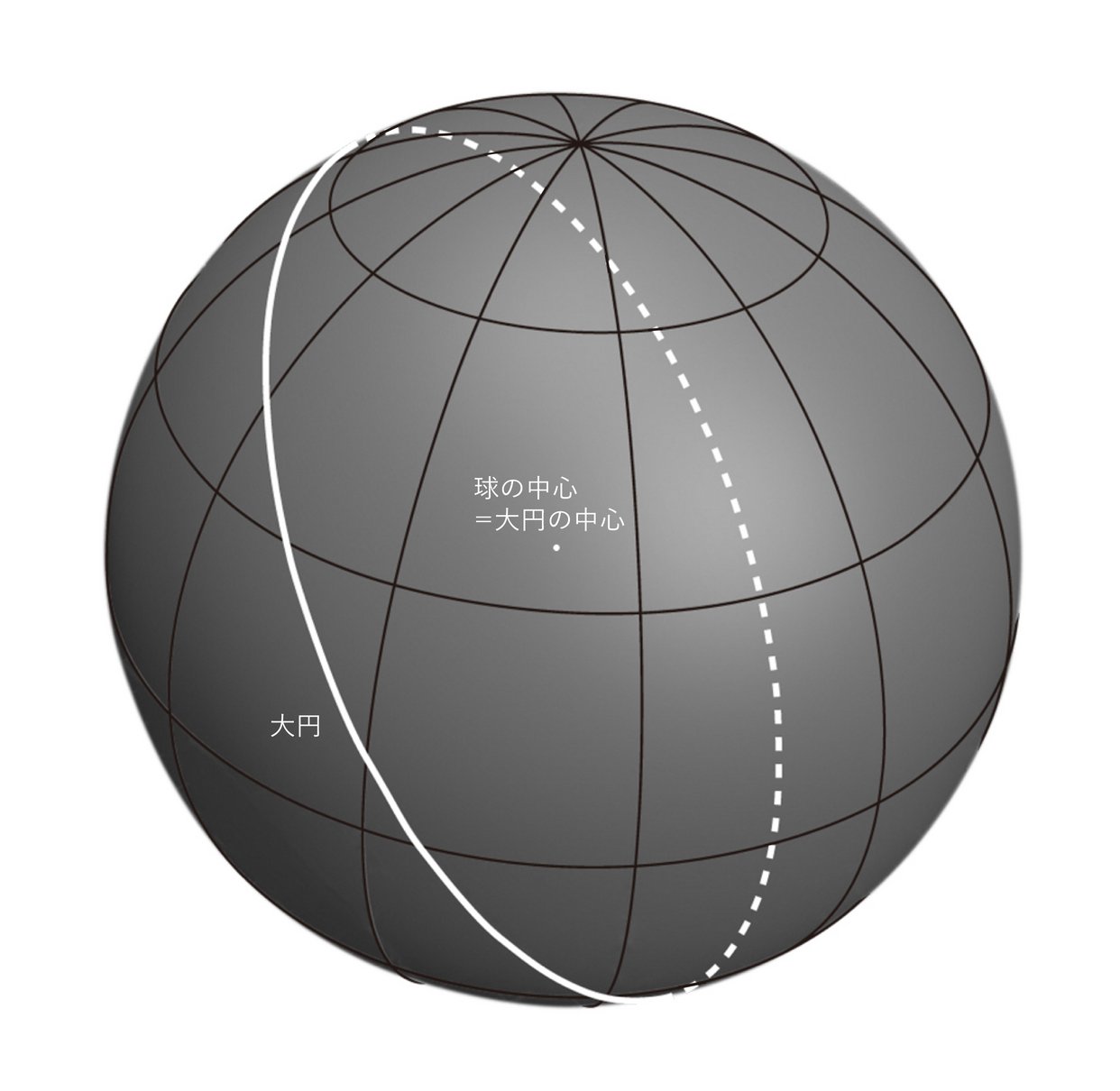
球面上の直線は「大円（だいえん）」の一部になっている。大円とは、球の中心を含むように球面を切ったときの断面である（図3）。球面をちょうど真っ二つに割ったときの断面だと言ってもいい。地球で言うと、東西の経度を表す経線はすべて大円、つまり球面上での直線である。一方、南北の緯度を表す緯線は、赤道（緯度0°）を除いて大円ではない、つまり球面上での直線ではないことになる。

今度は、球面と同じように曲がっている有限の宇宙（3次元空間）を考えてみよう。この場合も、まっすぐに引いた直線は、宇宙をグルっと一周して元の場所に戻ってくることになる。「直線が元の場所に戻ってくるなんてことはありえない。仮に元の場所に戻ってきてしまったとしたら、それは直線ではなく、曲がっているはずだ！」と考えたくなるかもしれない。この場合も鍵を握るのは、どうすれば、「まっすぐ」と言えるのか、である。

曲がった3次元空間における「まっすぐ（直線）」も、「2点間を結ぶ最短ルート」だと考えればよい。そして広大な宇宙で「最短ルート」を調べるのに使われるのが光だ。

上述した通り、空間は太陽の近くなどで部分的には曲がることが実証されている。では、広大な宇宙は全体として曲がっているのだろうか。

2次元の面である地球の表面が全体として曲がっていることは、宇宙から眺めれば一目瞭然だ。しかし、 私たちは宇宙空間を“外”から眺めることはできないので、宇宙空間が全体として曲がっているかどうかは確かめようがないようにも思える。しかし実は、宇宙空間の中にいながらにして、宇宙空間が全体的に曲がっているかどうかを確かめる方法がある。それは「広大な宇宙空間で三角形を考え、その内角の和（合計）が180°になるかどうかを調べる」という方法だ。

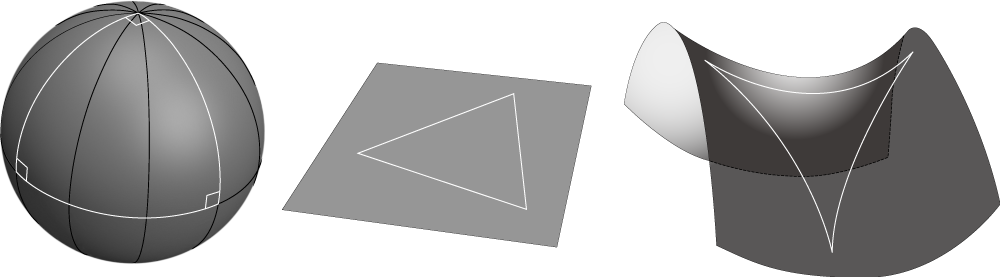
小学校で「三角形の内角の和は180°になる」と習ったことを覚えているだろうか。実はこの法則が成り立つには、ある条件が必要である。それは「三角形が描かれた面が平らである」という条件だ。三角形が描かれた面が曲がっていたら、三角形の内角の和は180°からずれてしまうのだ。

例えば、三角形が描かれた面が、曲がった球面だった場合、三角形の内角の和は180°より大きくなる。上述した通り、球面上での直線は大円または大円の一部であり、地球でいうと経線と赤道が直線に当たる。地球儀をもってきて、適当な2本の経線と赤道で三角形を作ってみてほしい。赤道と経線は必ず直交する、つまり90°で交わるので、赤道と経線が成す2つの角度を足すだけで180°になり、経線どうしが成す角度をさらに足すと必ず180°を超えることが分かるはずだ（図4）。

ただし、曲がった球面上でも、描いた三角形が小さいと180°からのずれは小さすぎて目立たない。私たちが地球の曲がりを実感できないのはこのためだ。

このように三角形の内角の和が180°を超えるような面は、「正（プラスの値）の曲率をもつ曲面」と呼ばれる（図5）。一方、三角形の内角の和が180°未満になるような面は、「負（マイナスの値）の曲率をもつ曲面」と呼ばれる。負の曲率の曲面の代表的なものは、馬の鞍のような曲面だ。三角形の内角の和がちょうど180°になるような面が平らな面（平面）であり、曲率はゼロになる。宇宙全体で曲がり具合（曲率）が一定だと仮定した場合、基本的には、曲率が正なら「有限の宇宙」に、曲率がゼロまたは負なら「無限の宇宙」になる。

宇宙空間（3次元空間）の曲がり具合は、宇宙スケールの三角形を考え、その内角の和を測ることで調べることができる。実際、それに相当する天文観測が行われており、観測可能な領域についてはほぼ平らだということが分かっている。ただし、測定には誤差があるので、完全に平らなのか、わずかに正または負の曲率をもっているのかについては何とも言えない。また、地球の表面の曲がりぐあいを私たちが見える範囲では実感できないように、観測可能な領域は宇宙全体の曲がりぐあいを調べるのには小さすぎるのかもしれない。そのため、宇宙が有限なのか、無限なのかは、完全決着がついていないのだ。

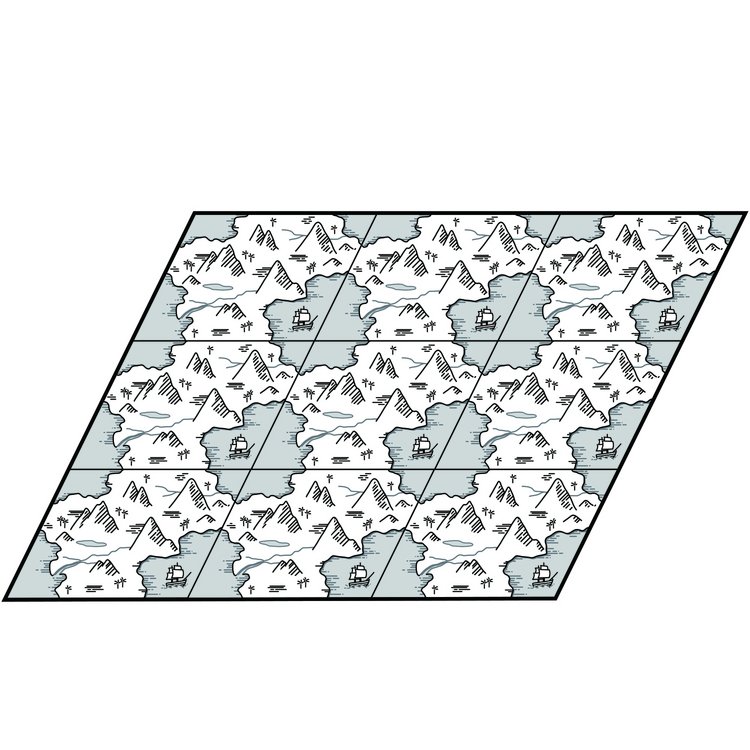
ここまでは、「体積が有限で、果てがない空間（＝有限の宇宙）」は、曲がって閉じている空間だという前提で話してきたが、厳密に言えば、「曲がっていない有限の宇宙」も、理論的には考えることができる。これもまた2次元の面で考えてみると、それはファミコン時代の「ドラゴンクエスト」などのRPG（ロールプレイングゲーム）のワールドマップのような世界になる。こういったゲームでは、操作キャラクターや船などの乗り物がマップの右端をこえると、左端から出てくる。これはマップの右の辺と左の辺が実は「同じもの」であることを意味している。つまり右の辺と左の辺が、空間を超えてくっついているわけだ（図6）。

このような世界を少し強引に立体的に描くと、ドーナツの表面のような形状の「トーラス」という面になる（図8）。正方形の左右の辺をくっつけると円筒になり、さらに円筒の上下をくっつけると、ドーナツの表面のような面になるのが分かるだろう。

次に「無限の宇宙」について考えてみよう。ここで言う「無限の宇宙」とは、「体積が無限大で、果てがない空間」のことである。

まず注意したいのが「無限大（∞）」の意味だ。無限大とは、「凄まじく大きい数」という意味ではない。無限大は、考えうるどんな数よりも圧倒的に大きいのだ。無限大にどんな数を足しても無限大のままだし（∞＋x＝∞）、無限大からどんな数を引いても無限大のままである（∞－x＝∞）。また、無限大にどんな正の数をかけても無限大のままだし（∞×x＝∞）、無限大をどんな正の数で割っても無限大のままである（∞÷x＝∞）。無限大を分母にした分数を考えると、分子にどんなに大きな数（たとえば、10^{10000000000000}）をもってきても、その分数の値はゼロである⁽⁴⁾。

また、どんなに起きる確率が小さい現象でも、無限回行えば、その現象は無限回起きる（∞×x＝∞なので。この場合、xは非常に小さい確率の値）。例えば、宝くじで1億円が当たる、といったことも、宝くじを無限回買うことができれば、必ず無限回起きることになる。

この考え方を無限の宇宙に適用すると、非常に奇妙なことが予言される。宇宙の遠いどこかには、地球と見分けのつかない惑星があり、そこにはあなたと見分けのつかない人間がいて、あなたと同じような人生を歩んでいることになるのだ。一見、突拍子もないことを言っているように思えるかもしれないが、論理的に考える限り、必然的にそんな結論になってしまうのだ。

地球や私たち人間を含め、身のまわりの物質は原子でできている。原子の中心には原子核があり、その周囲には「電子」が存在している。そして原子核は、「陽子」と「中性子」という2種類の粒子でできている。原子には、水素、炭素、鉄、ウランといったように100を超える種類があるが、あらゆる原子は、電子と陽子と中性子の3種類の粒子だけでできていることになる（原子の種類［元素］は、陽子の個数で決まる）。

さて、ここから言える重要なことは、「地球や私たち人間も含めて、身のまわりの物質の状態は、電子と陽子と中性子という3種類の粒子の状態（位置と速度）で決まっている」ということである⁽⁵⁾。今この瞬間のあなたという人間の状態（姿形や健康状態、心のありようなど）も、究極的にはこれら三つの粒子がどこに配置され、どの方向にどのくらいの速さで動いているか、で決まっているはずなのだ。

私たちの心が電子と陽子と中性子の状態だけで決まっているなんて、納得がいかないかもしれない。しかし心は、脳にある多数の神経細胞（ニューロン）の活動によって生じていると考えられており、これらの神経細胞の状態も結局のところ、電子と陽子と中性子の状態で決まっているはずだ。そのため、心もこれらの粒子の状態で究極的には説明できるはずだと考えられる。何ともドライな考え方であり、唯物論的、還元主義的な偏った見方だと思われるかもしれないが、魂のようなものの存在を仮定しない現代科学における標準的な見方だといえるだろう。

ミクロな世界を記述する物理学の理論である「量子論」によると、粒子の位置を無限に細かく決めることはできない。粒子の位置は常にある程度ぼやけているのだ。これはミクロな世界が、デジタル画像のようなものだということを意味している。

縦に画素が3つ、横に画素が3つある、計9画素のデジタル画像を考えよう。それぞれの画素は白または黒しか表示できないとする。このデジタル画像は、2×2×2×2×2×2×2×2×2＝2⁹＝512通りの画像を表すことができる。ここで重要なことは、画素がどんなに多くなっても、画像のパターンは有限の数にしかならない、ということだ。

観測可能な領域に存在する電子、陽子、中性子の配置パターンは膨大な数になるが、それでもデジタル画像の例と同様に有限の数になる⁽⁶⁾。デジタル画像での白の画素が「粒子が存在していない状態」、黒の画素が「粒子が存在している状態」に相当すると考えれば、その対応関係がイメージできるだろう。粒子は3種類あるので、計算はもっと複雑だが、配置パターンが有限の数になるという結論は変わらない。また、粒子の速度も位置と同じく、ミクロな世界ではぼやけてしまうので、取り得る状態のパターンはやはり有限の数になる。

以上を踏まえて考えると、私たちが住む観測可能な領域の今この瞬間の全粒子の状態が偶然実現する確率は非常に小さいが、取り得る状態のパターンが有限である以上、確率はゼロではない値になる⁽⁷⁾。

もし宇宙が無限に大きければ、観測可能な領域と同じ体積をもつ空間は無限に存在することになる。とすると、私たちが住む観測可能な領域と見分けがつかない粒子の状態になっている、同じサイズの空間は無限にあることになる。先に述べたように、どんなに小さな確率の現象でも、その確率がゼロでない限り、無限回繰り返せば、必ず無限回起きるからだ。私たちが住む観測可能な領域と見分けがつかない状態の領域には、地球と見分けがつかない惑星があり、あなたと見分けがつかない人間が住んでいることになる。しかも、そのような領域は無限個存在するのだ。

さらにいえば、私たちが住む観測可能な領域と、わずかに異なる領域も無限にあることになる。そこには、ほんの少し地球とは大陸の形が異なる惑星があり、あなたとほんの少し身長が異なり、ちょっとだけ違う人生を歩んでいる人間もいるだろう。

マサチューセッツ工科大学教授の理論物理学者、マックス・テグマーク博士が著書『数学的な宇宙』（講談社、2016年刊）で示している計算結果によれば、私たちが住む観測可能な領域と見分けがつかない領域は、10の10¹¹⁸乗メートル先にある、という計算になるのだという。数学の累乗の表記のマジックで一見、そこまで大きな数に見えないかもしれないが、これは途方もなく大きい数である。10¹¹⁸は、1の後に0が118個連なった数である。10の10¹¹⁸乗は、1の後に0が10¹¹⁸個連なった数である。もうあまりの大きさに笑うしかないだろう。

ここまで読んできて、宇宙は有限か無限か、あなたはどちらだと思っただろうか？　曲がって閉じている有限の宇宙も、あなたと見分けがつかない人間が無数に存在する無限の宇宙も、どちらも常識的な感覚からすると、なかなか信じがたいことだろう。しかし、常識的な感覚にしばられていては、宇宙の真理には近づけない。

最後にここまでの話をひっくり返してしまうようなことを敢えて言ってしまおう。実は私たちの住む宇宙は、見方によって無限に見えたり、有限に見えたりする、という考え方もある。これについては、後の回で詳しく解説することにしよう。

• 宇宙の体積は有限である可能性も、無限である可能性もある。
• 空間は曲がりうる。
• 宇宙は全体として、①球面のような曲がり方をしている（曲率が正）、②鞍のような曲がり方をしている（曲率が負）、③平ら（曲率がゼロ）――という三つの可能性がある。①の場合は有限の宇宙、②と③の場合は無限の宇宙になる。
• 天文観測によると、観測可能な領域はほぼ平らであることが分かっている。しかし、わずかに正または負の曲率をもっている可能性は残っている。
• 宇宙の体積が無限だった場合、宇宙のどこかに地球と見分けがつかない惑星、あなたと見分けがつかない人間が存在することになる。

1. ここで言う「宇宙空間の果て」は、第1回で紹介した「観測できる限界」という意味での「観測可能な宇宙の果て」とは異なる。空間がある場所で突然途切れている、といった状況のことを指している。

2. 宇宙論の分野では、「宇宙は大きなスケールで見れば一様であり、等方的（方向による違いがない）である」と基本的には考える。これを「宇宙原理」と呼ぶ。もう少しざっくりと言うと、「宇宙に特別な場所はなく、どこも同等である」ということだ。宇宙空間に果てがあると、宇宙原理に反してしまうことになる。

3. 質量は「重さ」と似ているが、別の概念である。重さとは、物体に働く重力の大きさのことだ。同じ物体でも天体が変われば、重さは変わる。例えば、月の重力は地球の約6分の1なので、地球で重さが60キログラム重の人が月に行くと、重さは約10キログラム重になる。一方、質量はその物体固有の量なので、どこに行っても値は変わらない。質量とは、その物体の加速のしにくさを表す量だと言える。物体の重さは、物体の質量に比例するという性質がある。

4. 厳密に言うと、無限大は数ではないので、単純な足し算や引き算、かけ算や割り算の対象とすべきではなく、高校数学で習う「極限」という考え方を使って計算するのが適切である。

5. 厳密に言うと、「量子論」という、ミクロな世界を記述する物理学の理論にもとづいて、各粒子の状態（量子状態）を考えるのが、より適切である。

6. ただし量子論によると、各状態（粒子の配置パターンに相当）の重ね合わせを考えることによって、さらに異なる状態を考えることもできる。量子論における「重ね合わせ」については連載の後の回で詳しく解説する予定だ。

7. 宇宙には、電子、陽子、中性子以外にも、様々な粒子が存在しているので、厳密に言えば、それらまで含めて考える必要がある。